Koç Lab - Projects

 Koç Lab  
 Founder  
 People  
 Projects  
 Publications  
 News  

Finite Field Arithmetic

All public-key cryptographic functions, such as public-key encryption and decryption operations, digital signature generation and verification operations, homomorphic functions, variety of cryptographic protocols, and post-quantum cryptographic functions, are based on the arithmetic of number and polynomial groups, rings and fields. Mathematical properties of these structures, efficient representations of their elements, and algorithms for arithmetic operations need to be well understood in order to design suitable software and hardware. This endeavor is in a way similar to the design and implementation of error-detecting and error-correcting codes, however, in cryptography the lengths of the elements are significantly larger.

The primary operation for the PKC algorithms is the exponentiation or point multiplication operation in the group built upon the finite field or ring arithmetic. Cryptographic protocols aim to minimize field and ring operations for efficiency, without sacrificing security. On the other hand, efficient finite field and ring arithmetic leads to efficient public-key cryptography. This is an interdisciplinary research area, involving mathematics, computer science, and electrical engineering.
The basic arithmetic operations used in PKC are the addition, subtraction and multiplication operations in finite fields. These basic functions can be designed into an ALU so that they are available for use in various cryptographic algorithms and protocols. By designing a data path and an instruction set architecture, we can create a cryptographic processor or co-processor on a given computational platform. More complicated functions such as finite field inversion, exponentiation, elliptic curve point addition, and elliptic curve point multiplications can use these basic functions repeatedly with the help of finite state machines. The complexity of the PKC ALU design is determined by the portfolio of the basic functions and the width of the data path. We need to build a computational pyramid.
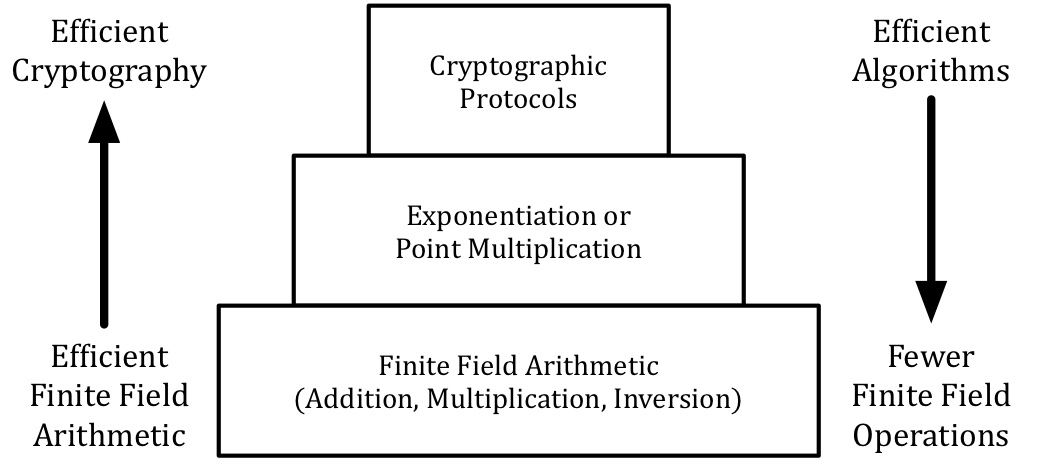
We have made significant contributions to finite field arithmetic, and continue to invent new algorithms and architectures.

Selected Publications

  • Ç. K. Koç. Algorithms for inversion mod p^k. IEEE Transactions on Computers, 69(6): 907-913, June 2020.   pdf
  • W. Dai, D. D. Chen, R. C. C. Cheung, and Ç. K. Koç. Area-time efficient architecture of FFT-based Montgomery multiplication. IEEE Transactions on Computers, 66(3):375-388, March 2017.   pdf
  • D. D. Chen, G. X. Yao, R. C. C. Cheung, D. Pao, and Ç. K. Koç. Parameter space for the architecture of FFT-based Montgomery modular multiplication. IEEE Transactions on Computers, 65(1):147-160, January 2016.   pdf
  • Ç. K. Koç. Introduction to the Journal of Cryptographic Engineering. Journal of Cryptographic Engineering, 1(1):1-3, April 2011.   pdf
  • E. Savaş and Ç. K. Koç. Finite field arithmetic for cryptography. IEEE Circuits and Systems Magazine, 10(2):40-56, 2010.   pdf
  • A. F. Tenca, E. Savaş, and Ç. K. Koç. A design framework for scalable and unified multipliers in GF(p) and GF(2^m). International Journal of Computer Research, 13(1):68-83, 2004.   pdf
  • A. F. Tenca and Ç. K. Koç. A scalable architecture for modular multiplication based on Montgomery's algorithm. IEEE Transactions on Computers, 52(9):1215-1221, September 2003.   pdf
  • Ç. K. Koç and T. Acar. Montgomery multiplication in GF(2^k). Designs, Codes and Cryptography, 14(1):57-69, April 1998.   pdf

→   Random Number Generators